Un diagrama de círculo unitario es una plataforma utilizada para explicar la trigonometría. Puede usarlo para explicar todas las medidas posibles de ángulos desde 0 grados hasta 360 grados. Describe todos los ángulos negativos y positivos en el círculo.
En resumen, muestra todos los ángulos posibles que existen. Un círculo proporciona un rango mucho más amplio para medir ángulos. Es por eso que la gente usa esta forma en lugar de un triángulo rectángulo.
En un círculo unitario, mides los ángulos positivos usando el lado inicial del eje x positivo. Luego te mueves hacia el lado de la terminal. Hágalo en sentido contrario a las agujas del reloj alrededor del punto de origen.
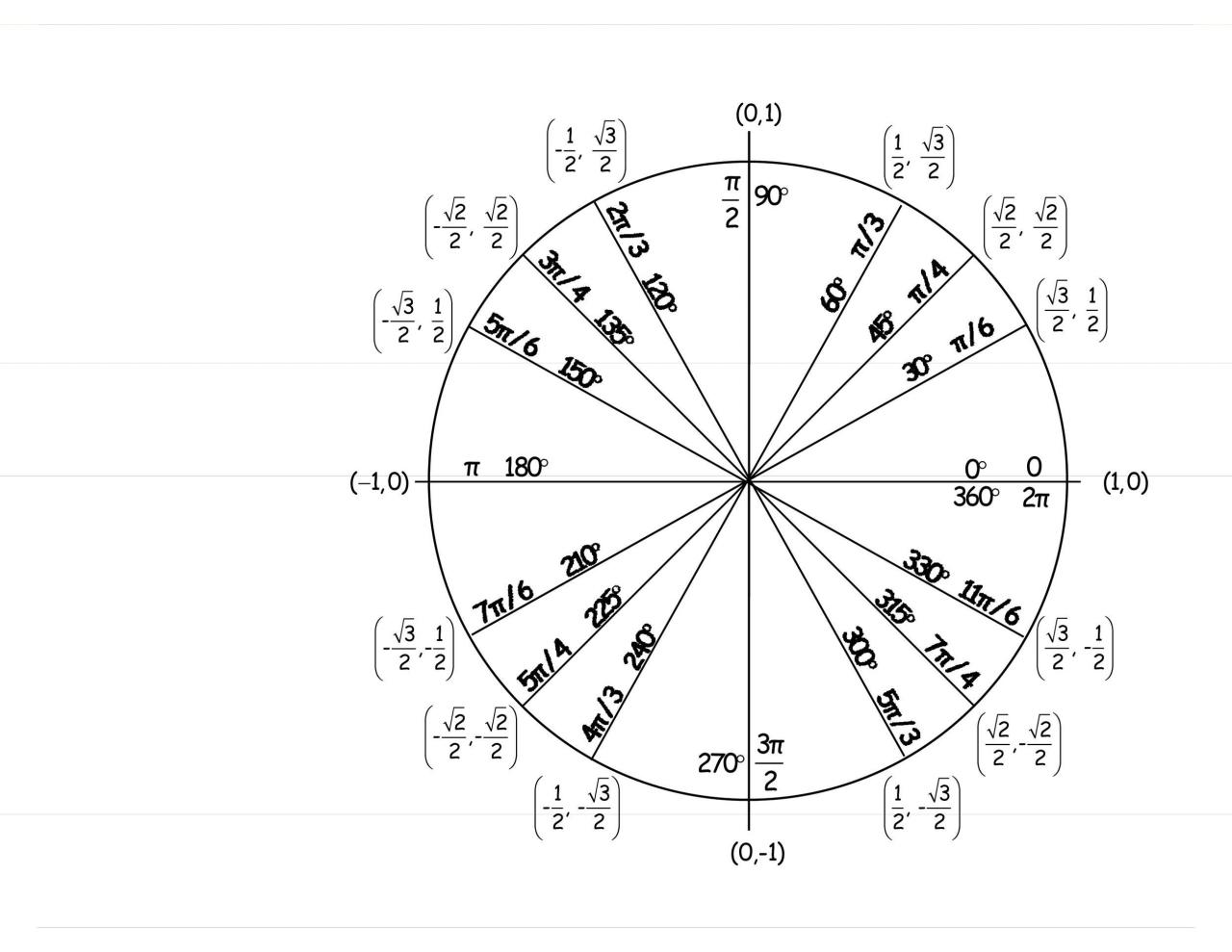
El diagrama mostraría ángulos positivos etiquetados en radianes y grados. Los lados terminales de los ángulos forman líneas rectas. Algunos ejemplos de estas medidas de ángulo son 30 y 210 grados, 60 y 240 grados, etc.
Este es un hecho que se espera cuando los ángulos están separados por 180 grados. Esto se debe a que los ángulos rectos miden 180 grados. Cuando utilice un gráfico de círculo trigonométrico/círculo trigonométrico, podrá ver la relevancia de este hecho.
Gráficos de círculos unitarios
![]()
#01
![]()
#03
![]()
#04
![]()
#05
![]()
#06
![]()
#07

![]()
#08
![]()
#09
Aparte de los ángulos positivos, los gráficos circulares unitarios o en radianes también muestran ángulos negativos. De hecho, muchos ángulos básicos tienen valores negativos y múltiplos de sí mismos. Para obtener estos valores, debe medir los ángulos en el sentido de las agujas del reloj.
Por ejemplo, un ángulo de 30 grados es lo mismo que un ángulo de -330 grados. Esto se debe a que sus lados terminales son iguales.
Sin embargo, hay más formas de nombrar ángulos. Cuando realiza una rotación completa del círculo, puede obtener infinitas medidas de ángulo. Puede hacer esto cuando suma o resta 360 grados durante la rotación.
Haga esto antes de decidirse por el lado terminal del ángulo . Entonces puedes obtener valores positivos y negativos del mismo ángulo básico.
¿Ya te confundes? Aclaremos con un ejemplo. Si tienes un ángulo que mide 60 grados, tendría el mismo lado terminal que los otros ángulos. Estos ángulos son el ángulo de 420 grados y el ángulo de -300.
De hecho, el mismo ángulo de 60 grados tendría muchos nombres diferentes tanto en radianes como en grados.
Puede pensar que los diferentes nombres de ángulos son simplemente inútiles y confusos. Pero hay más en estos diferentes nombres. Los ángulos conectados entre sí tienen funciones trigonométricas que también están conectadas, si no son iguales.
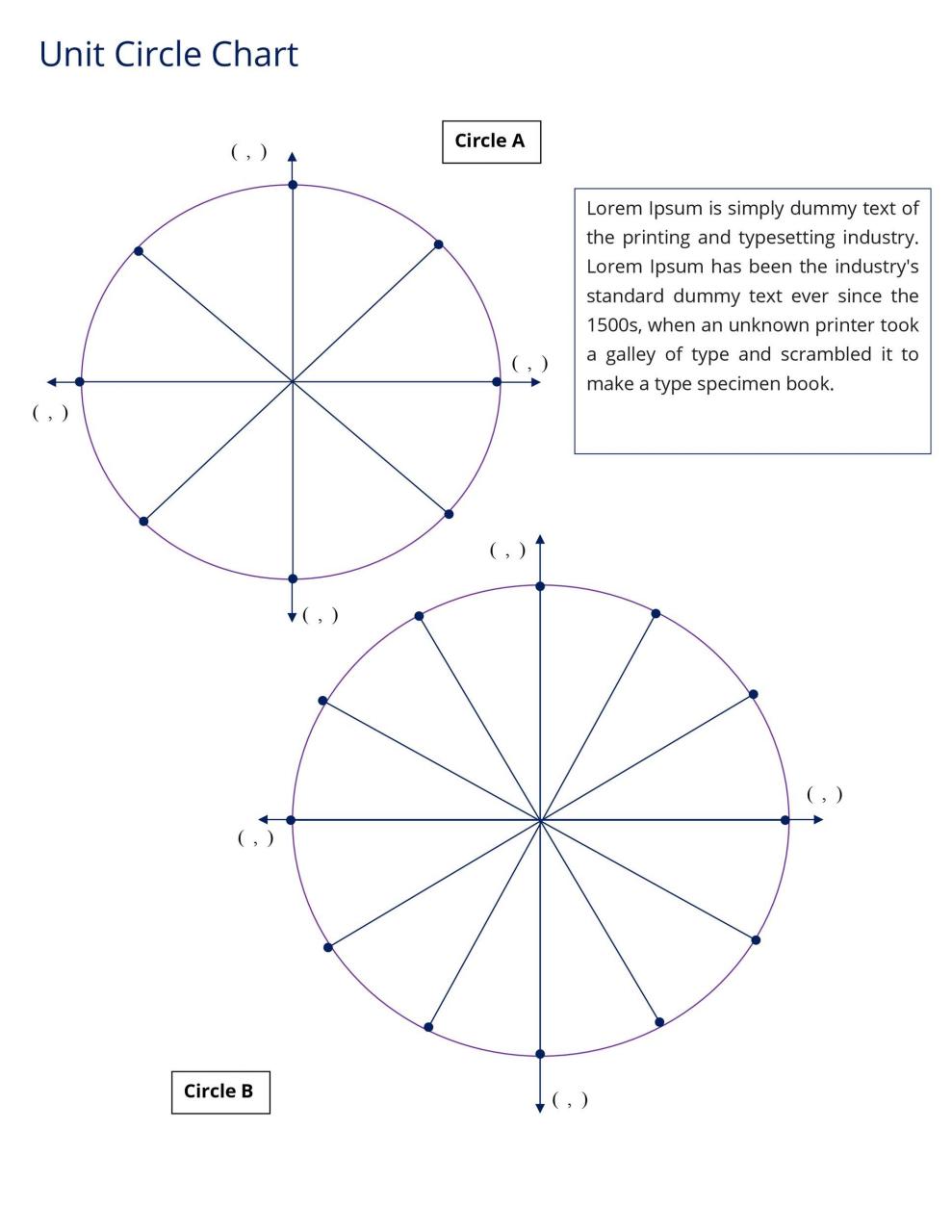
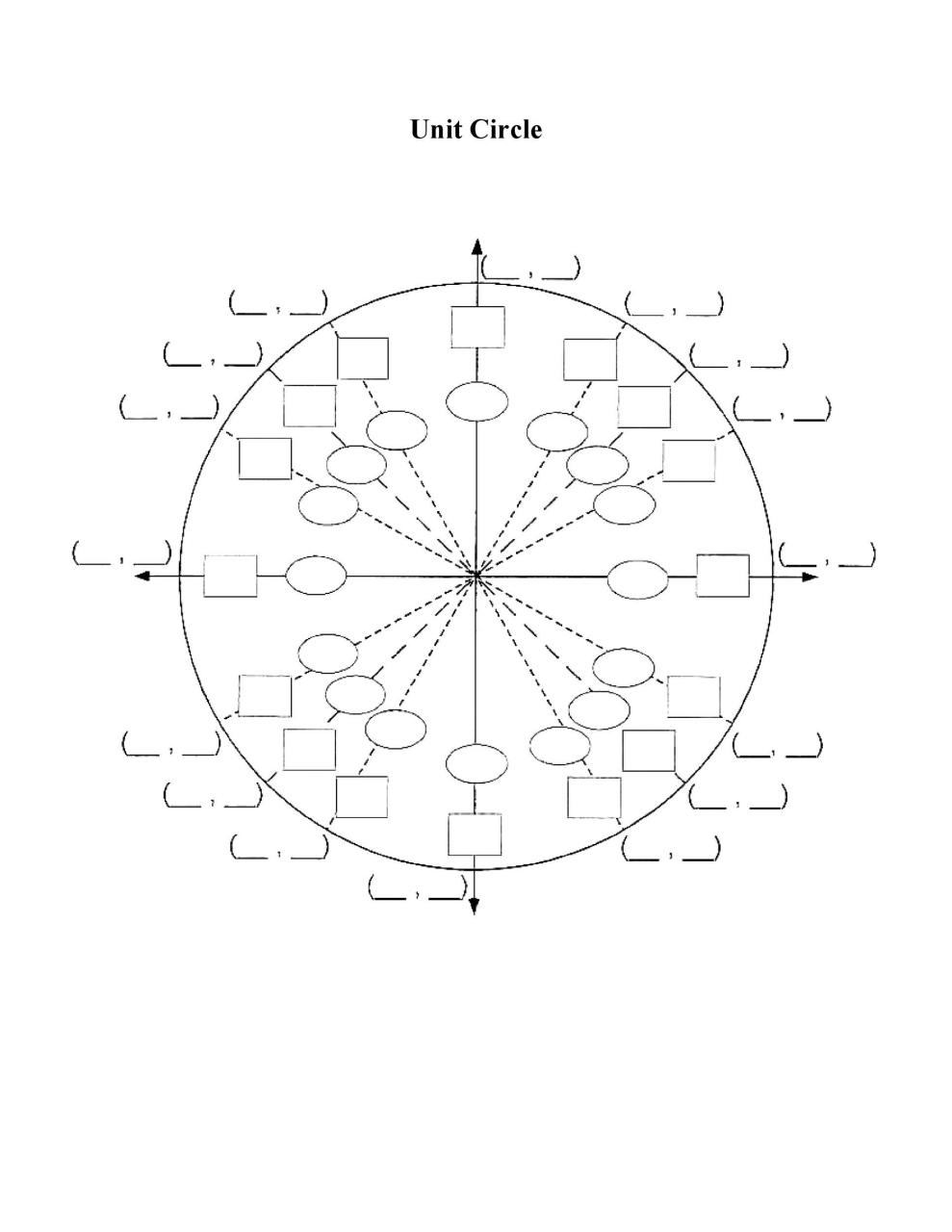
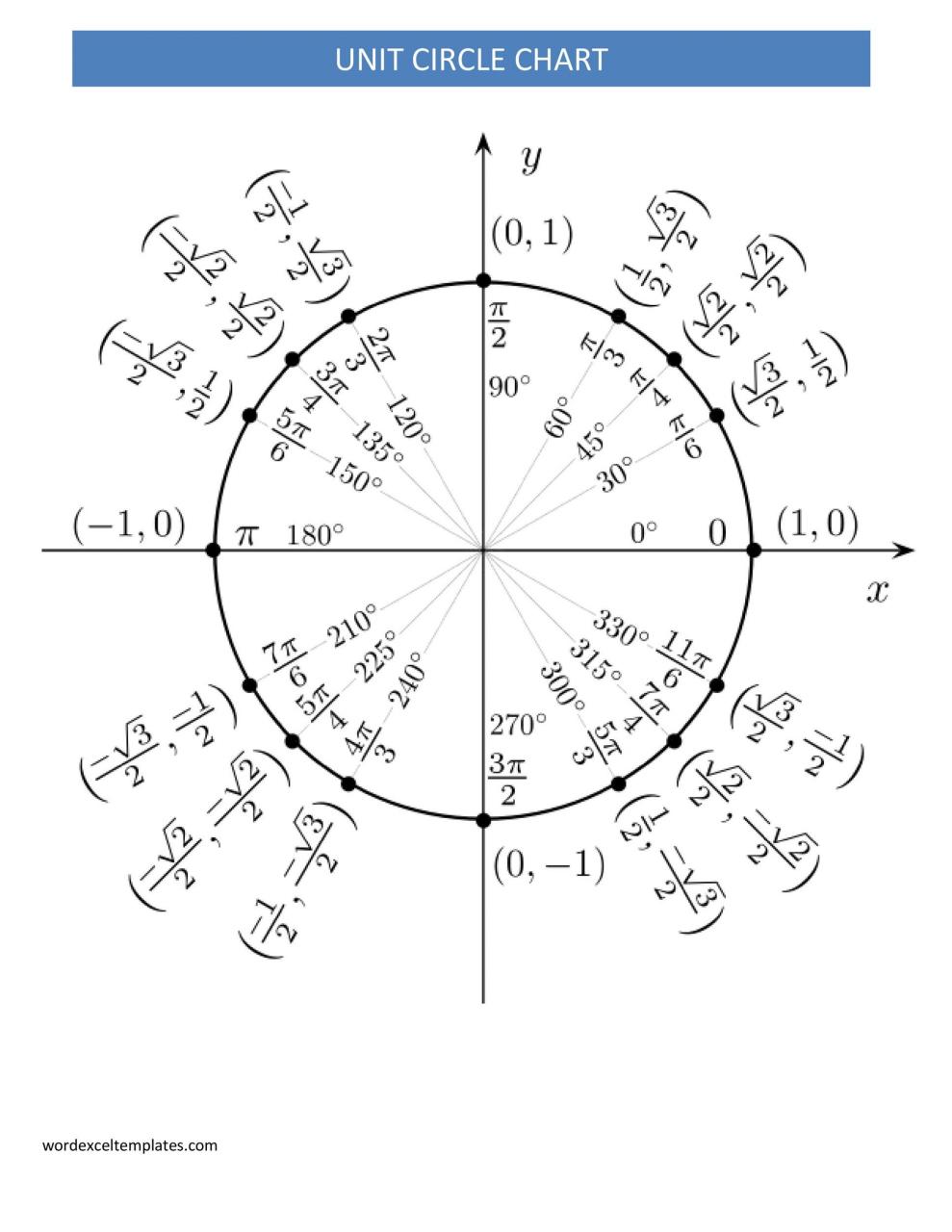
Diagramas de círculo unitario

![]()
#10
![]()
#11
![]()
#12
![]()
#13

![]()
#14
![]()
#15
![]()
#dieciséis

![]()
#17
![]()
#18

![]()
#19
Creación de un gráfico de círculo unitario
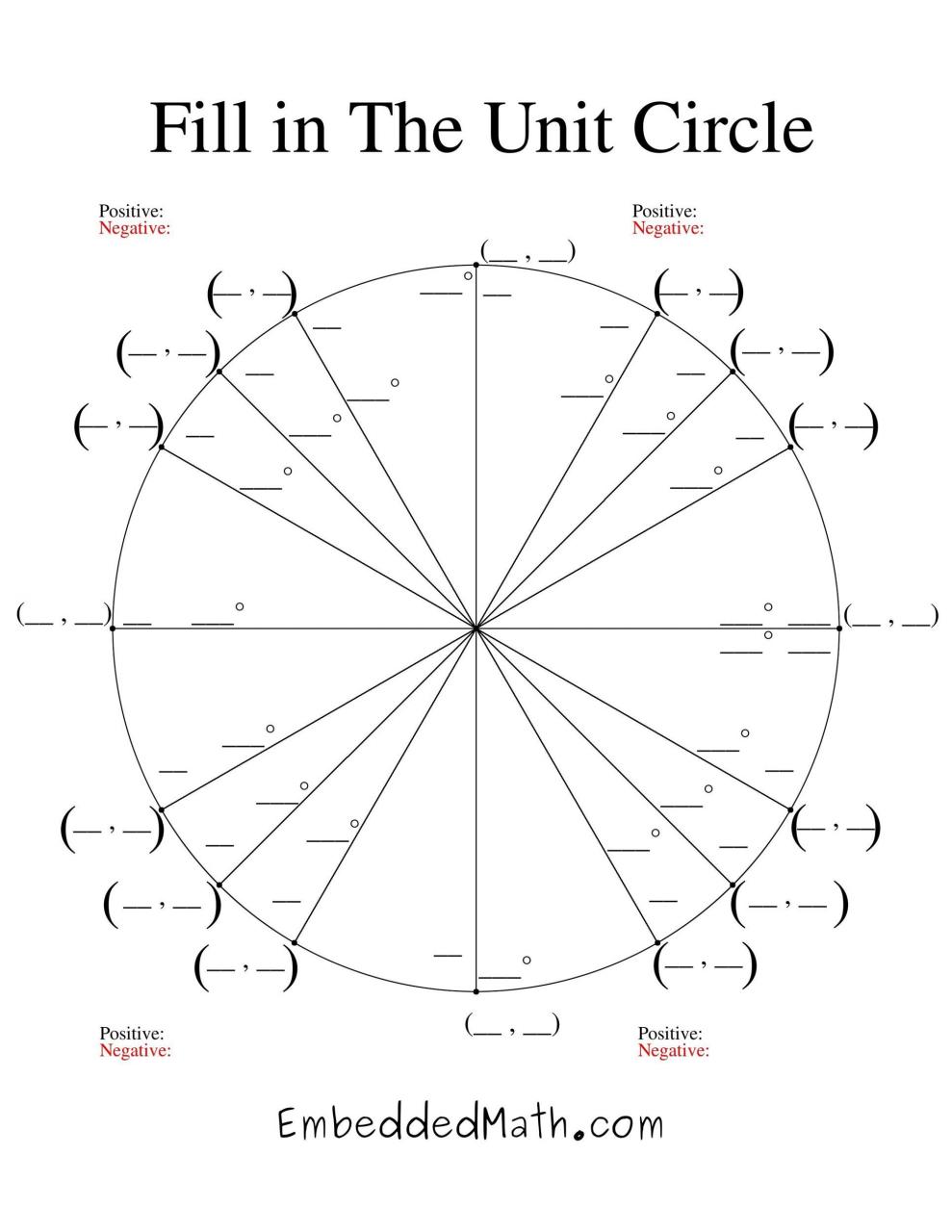
Aunque pueda parecer confuso, crear un diagrama de círculo unitario es bastante simple. Eso si tienes todos los pasos para hacerlo. De lo contrario, puede descargar un círculo unitario imprimible y trabajar con eso. Toma todos los triángulos rectángulos y los ángulos del círculo unitario. Luego júntelos, esto creará el círculo unitario completo. Mientras hace esto, necesita crear triángulos especiales uno a la vez. Debe hacer esto ya que todos son puntos específicos en un plano de coordenadas.
No importa qué tan largos sean los lados que uses para el ángulo en un triángulo, los valores de la función trigonométrica seguirán siendo los mismos. Para facilitar las cosas, los matemáticos redujeron todos los lados del triángulo.
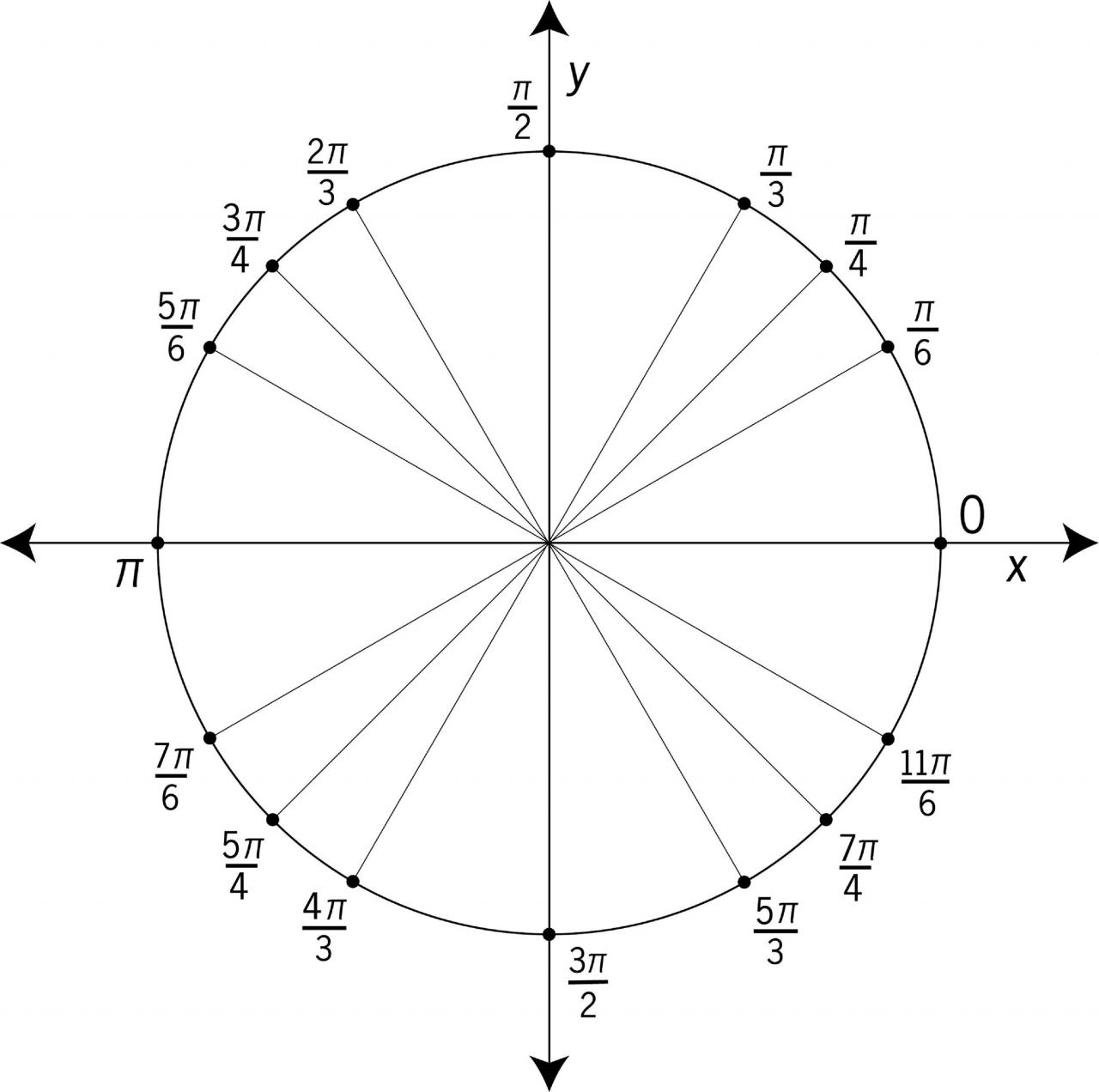
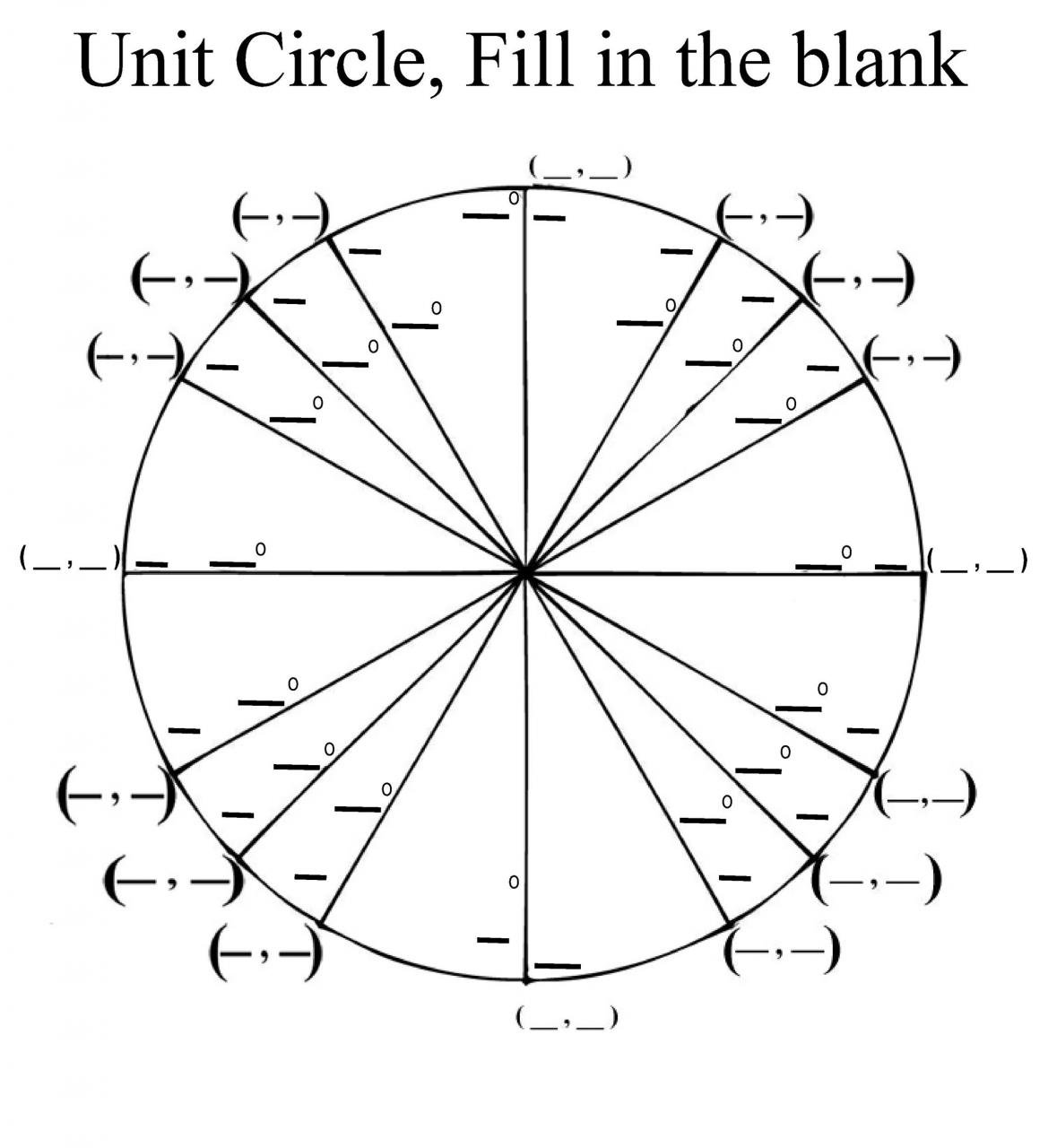
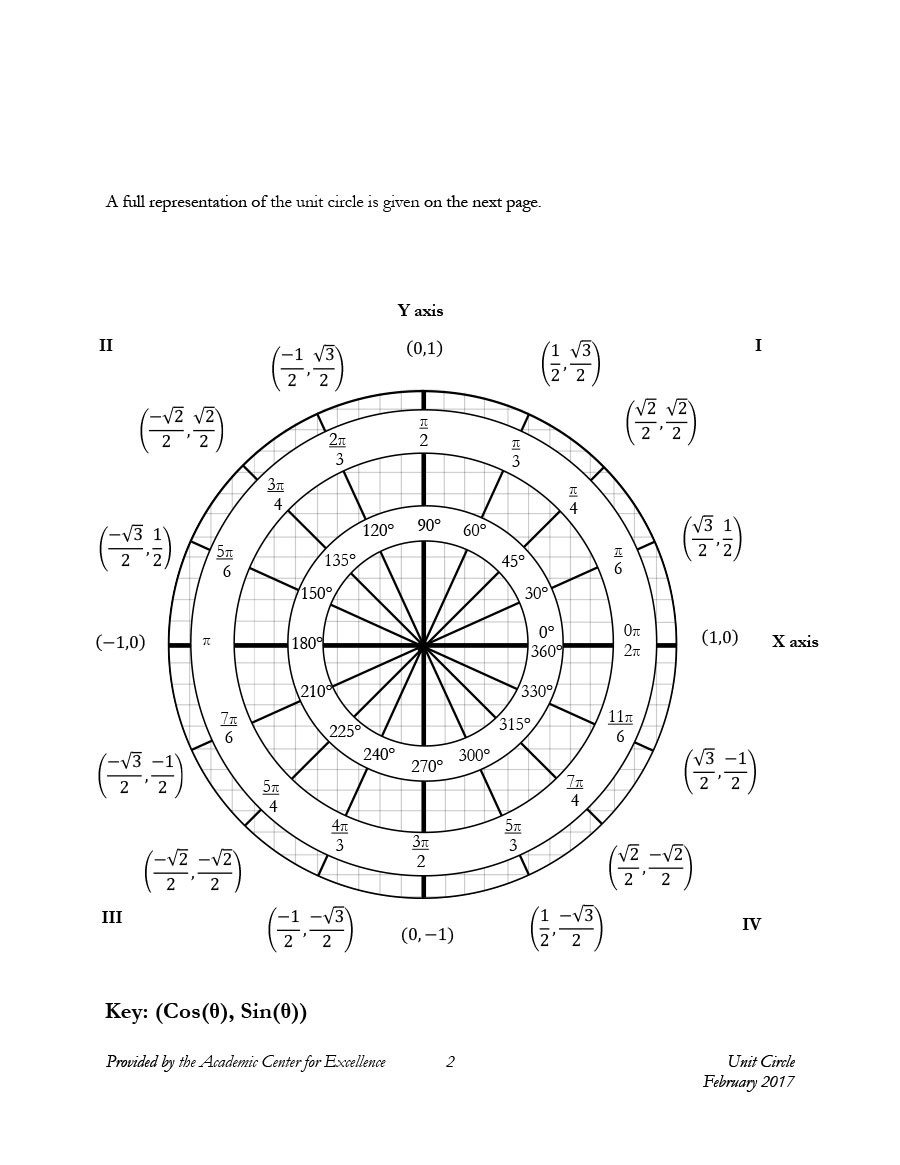
Imprimibles de círculo unitario
![]()
#20
![]()
#21
![]()
#22

![]()
#23
![]()
#24
![]()
#25

![]()
#26

![]()
#27

![]()
#28
![]()
#29
Hicieron esto para que todos los ángulos encajaran en todo el círculo unitario. Aquí hay algunos consejos que puede usar para hacer su propio gráfico circular de unidades o radianes:
- Comience en el primer cuadrante de un gráfico. En ese cuadrante, haz un ángulo de 30 grados para tu círculo unitario.
- Dibuja el ángulo con cuidado y conéctalo al origen con el uso de una línea recta.
- Asegúrate de que el lado terminal de tu ángulo de 30 grados esté en el primer cuadrante. Además, asegúrese de que el tamaño del ángulo sea bastante pequeño. Debe ser solo un tercio del camino entre 0 y 90 grados.
- Luego, dibuja una línea perpendicular. Al hacer esto, podrás crear un triángulo rectángulo.
- La hipotenusa del triángulo serviría como el radio de tu círculo unitario. Una de las piernas estaría en el eje x mientras que la otra pierna estaría en el eje y.
- Luego, necesitas encontrar la longitud de la hipotenusa. Ten en cuenta que con un círculo unitario, el radio siempre es 1. Esto significa que la hipotenusa del triángulo también sería 1.
- También necesitas encontrar la longitud de los otros lados del triángulo. Para hacer esto, comience con el lado más corto. Encuentra la longitud dividiendo el valor por 2. Para el lado largo, debes multiplicar el valor del lado corto por 2.
- Después de esto, necesitas identificar el punto en tu círculo. Un círculo unitario está en un plano coordinado que tiene el origen en su centro. Entonces, cada punto en el círculo tiene coordenadas distintas. A estas alturas, debería poder asignar un nombre al punto en el ángulo de 30 grados en su círculo unitario.
- Una vez que hayas realizado todos estos pasos, también será mucho más fácil encontrar los puntos de los otros ángulos en tu círculo.
- Tengamos un ejemplo. Encuentre el punto en su gráfico de círculo unitario marcado con 45 grados. Usa ese punto para dibujar un triángulo. Puede hacerlo utilizando el primer y segundo paso.
La hipotenusa del triángulo seguiría siendo 1, que también es el radio de tu círculo unitario. Una vez que hayas dibujado tu triángulo, puedes comenzar a encontrar las longitudes de los lados. Después de esto, puedes nombrar este punto en tu círculo unitario. - Los cuadrantes segundo y cuarto son simplemente imágenes especulares del cuadrante 1. Sin embargo, los signos difieren porque los puntos del círculo están en distintas ubicaciones del plano.
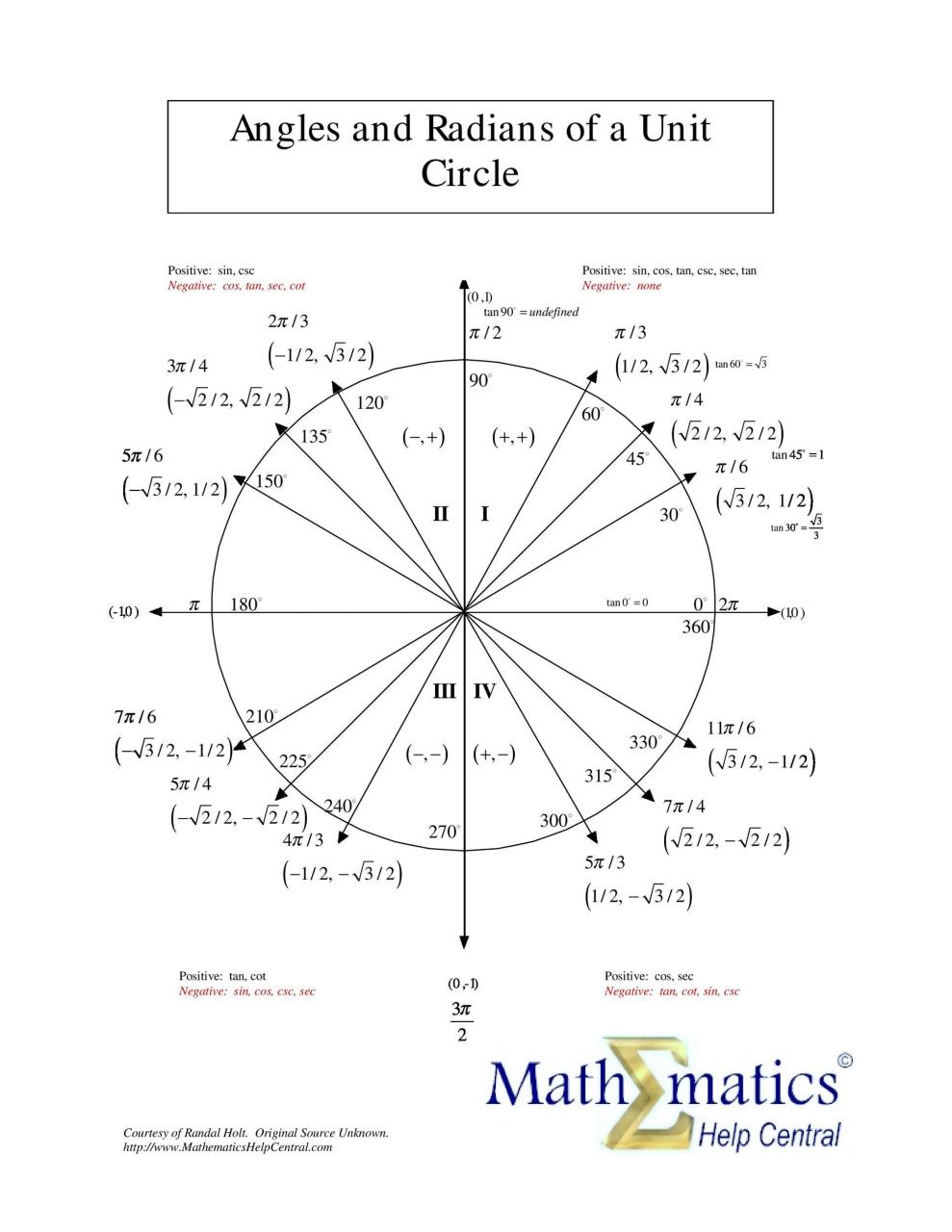
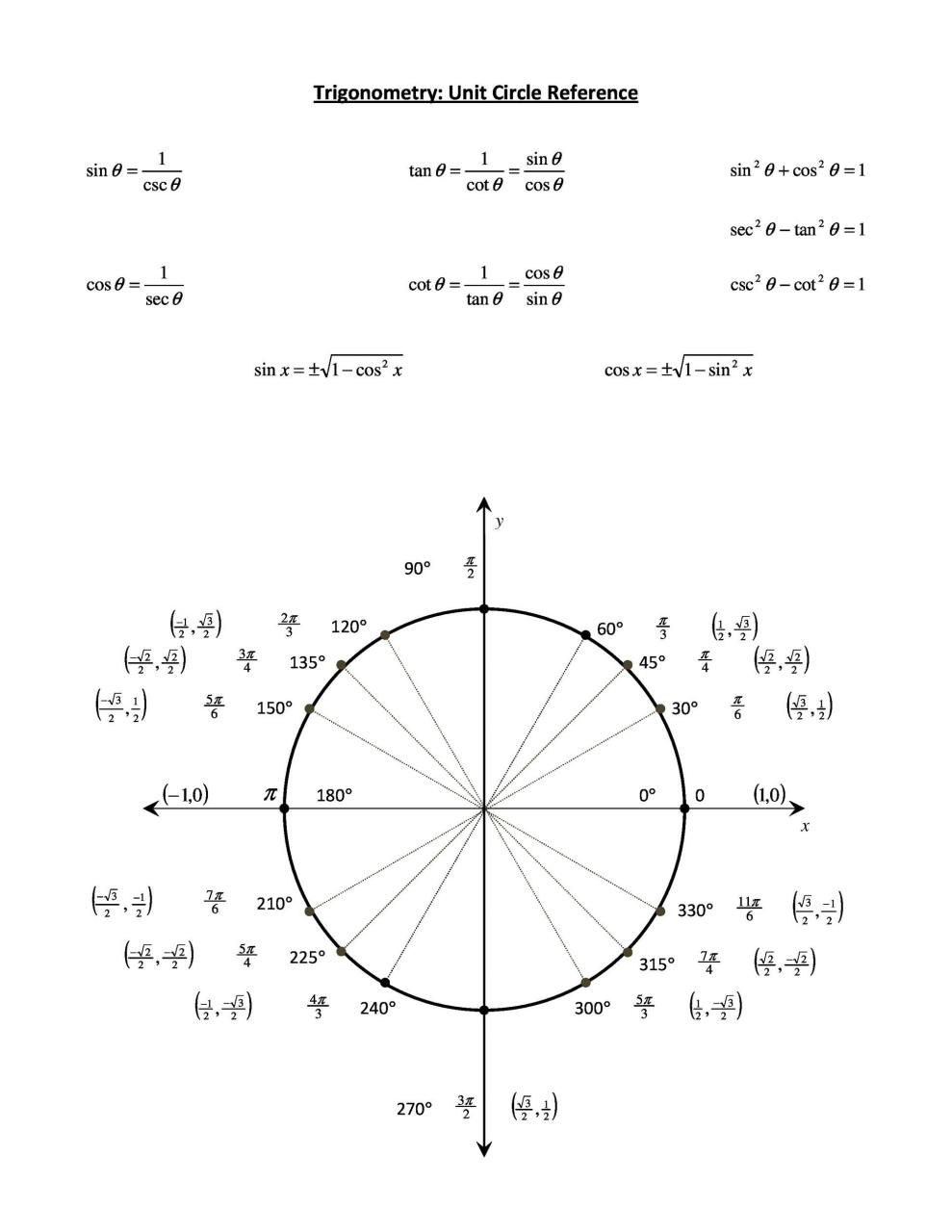
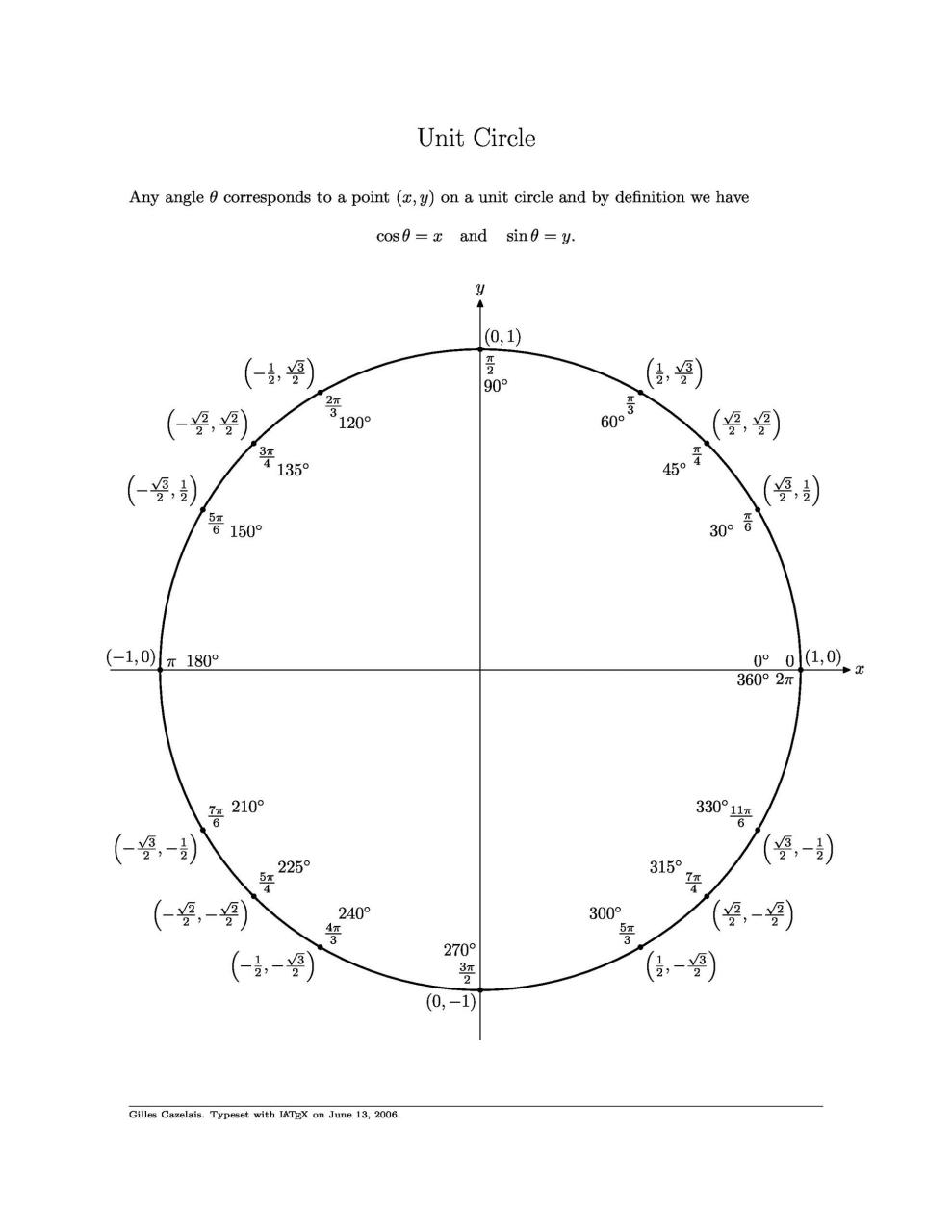
Gráficos circulares en radianes
![]()
#30
![]()
#31
![]()
#32
![]()
#33

![]()
#34

![]()
#35
![]()
#36
![]()
#37

![]()
#38
![]()
#39
![]()
#40
![]()
#41
![]()
#42
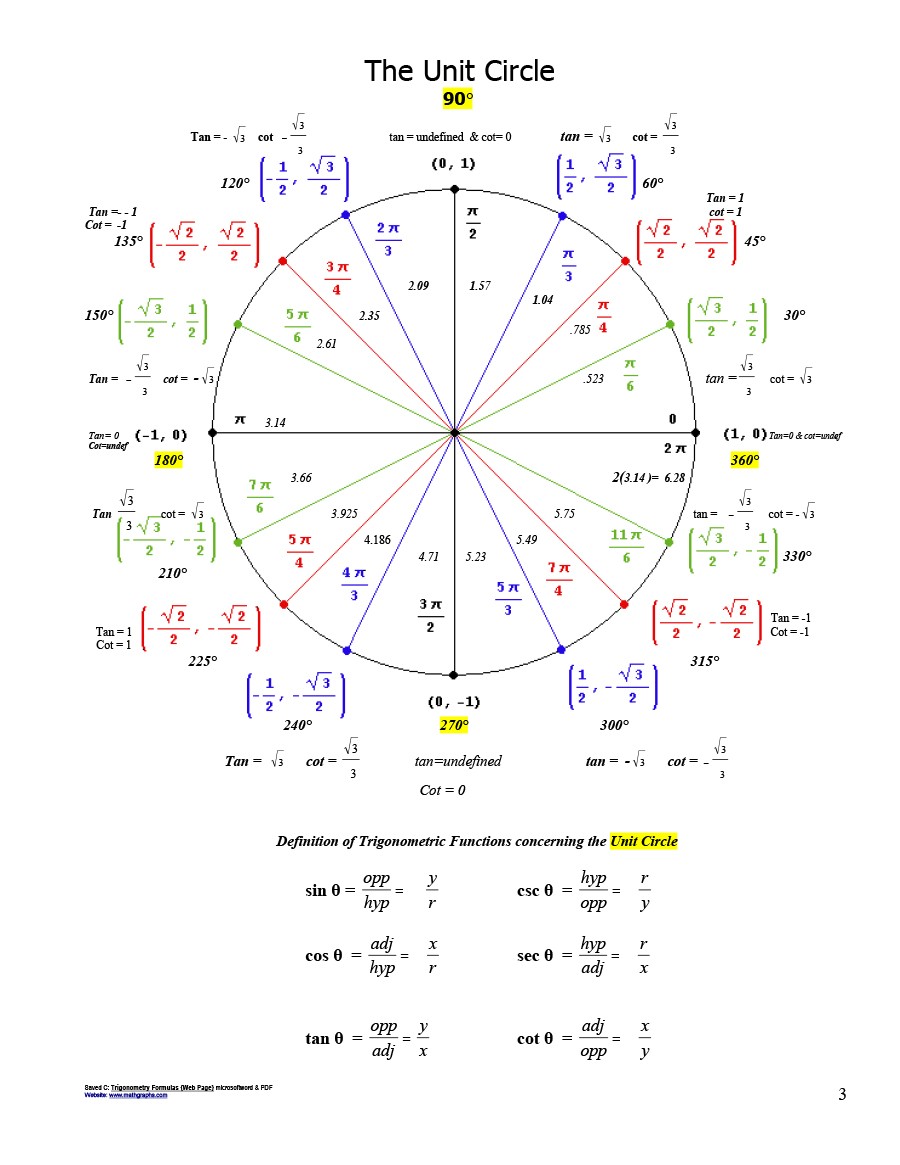
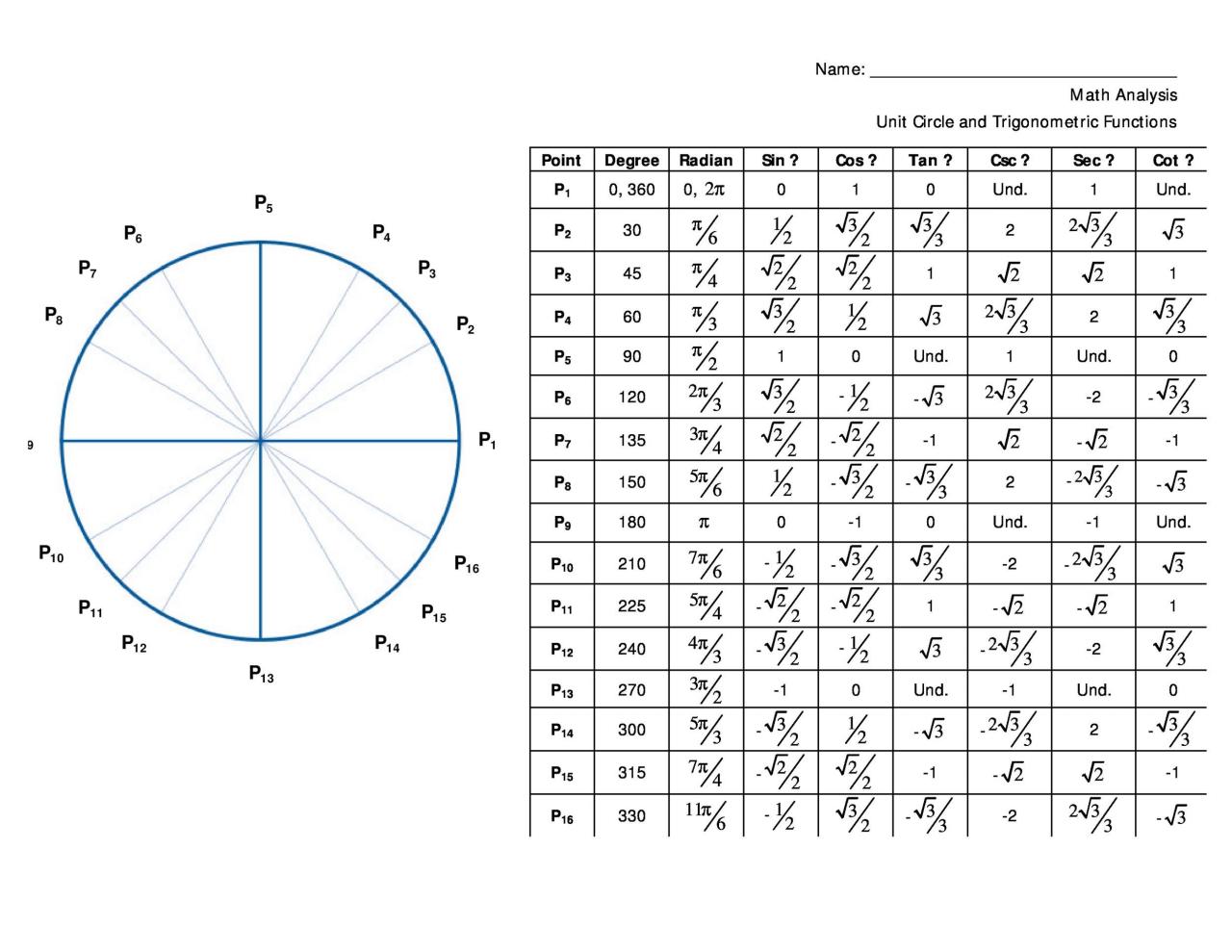
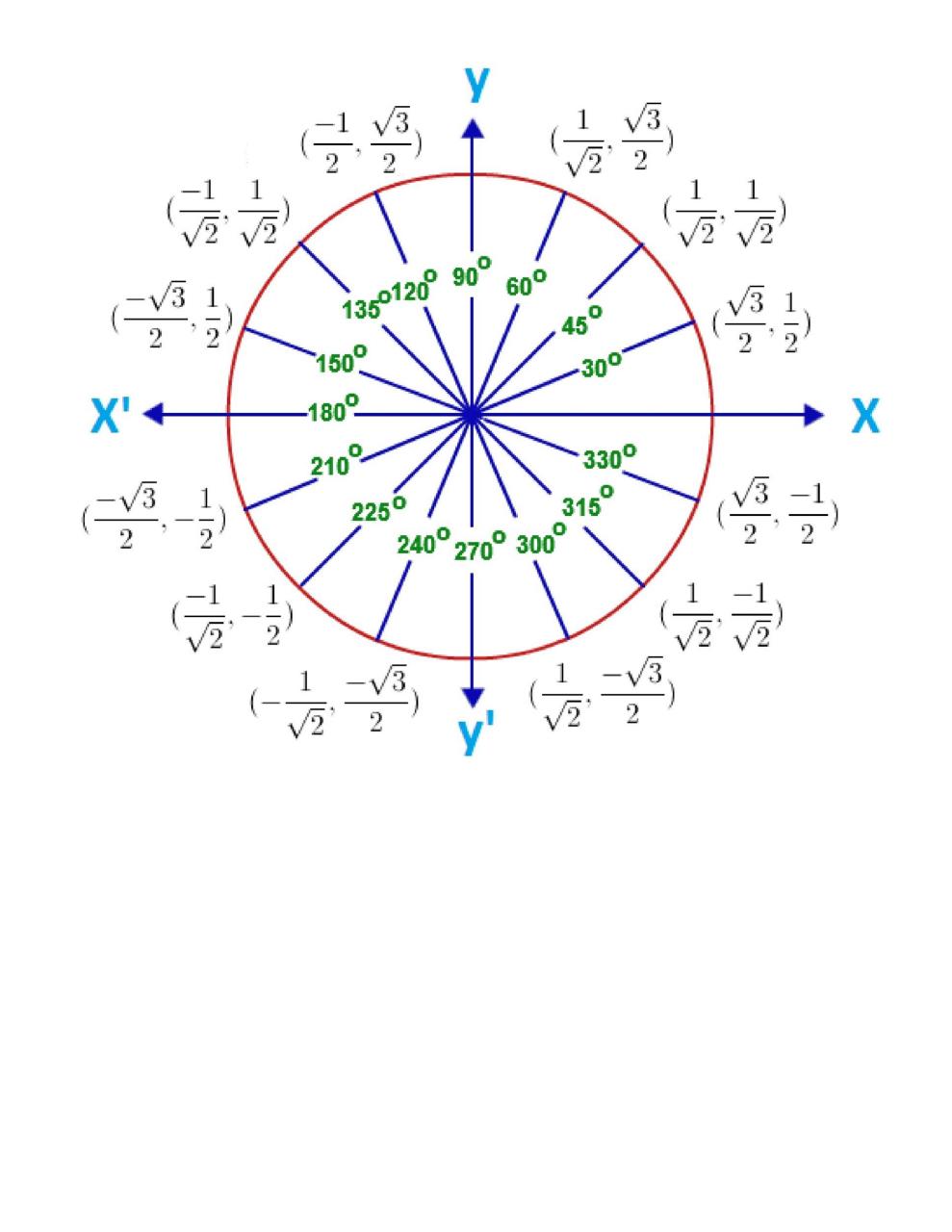
Aquí hay algunos datos que necesita saber sobre un gráfico de círculo trigonométrico/círculo trigonométrico:
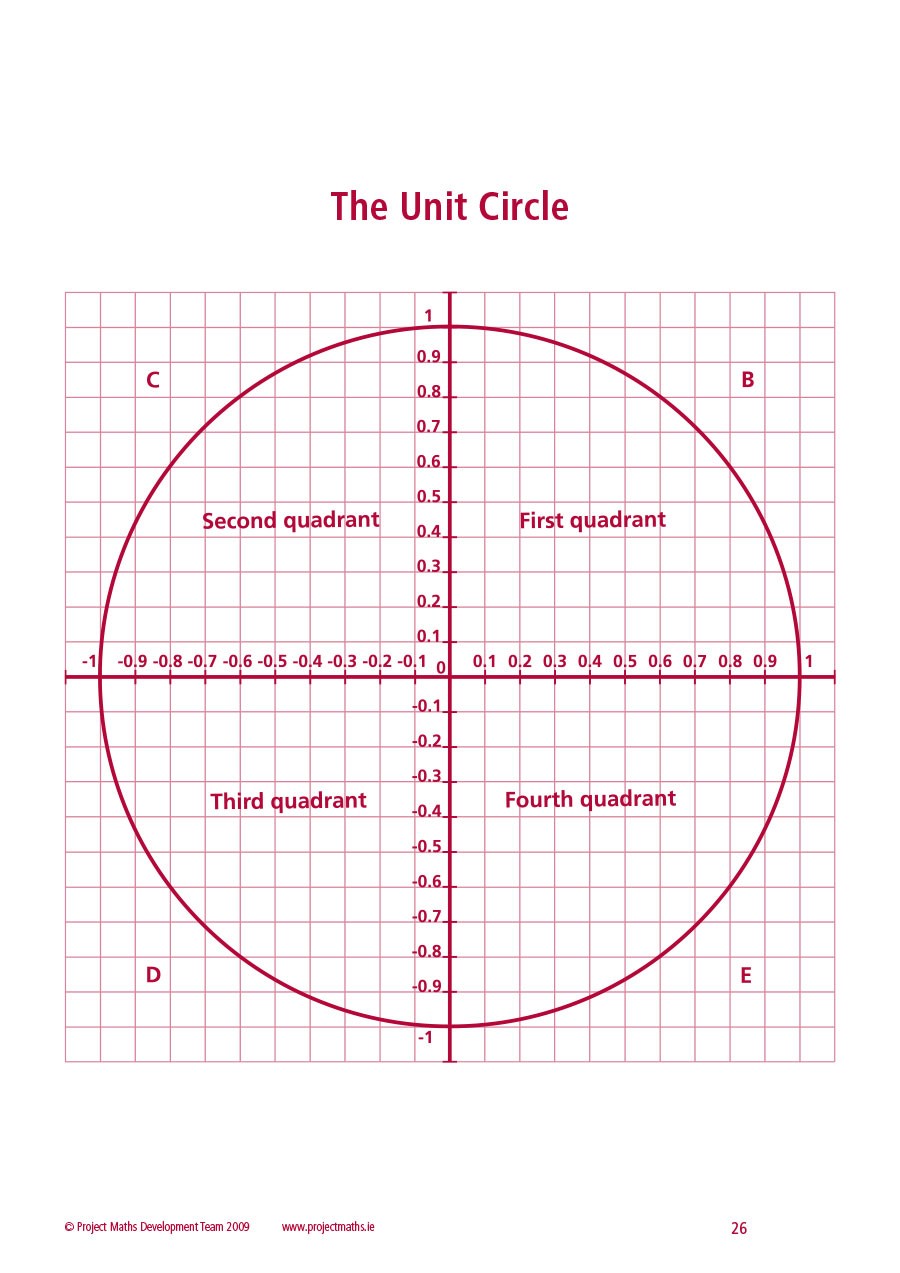
- En el primer cuadrante, tendrá valores positivos de x e y.
- En el segundo cuadrante, tendrá un valor de x negativo y un valor de y positivo.
- En el tercer cuadrante, tendrá valores negativos de x e y.
- En el cuarto cuadrante, tendrá un valor de x positivo y un valor de y negativo.
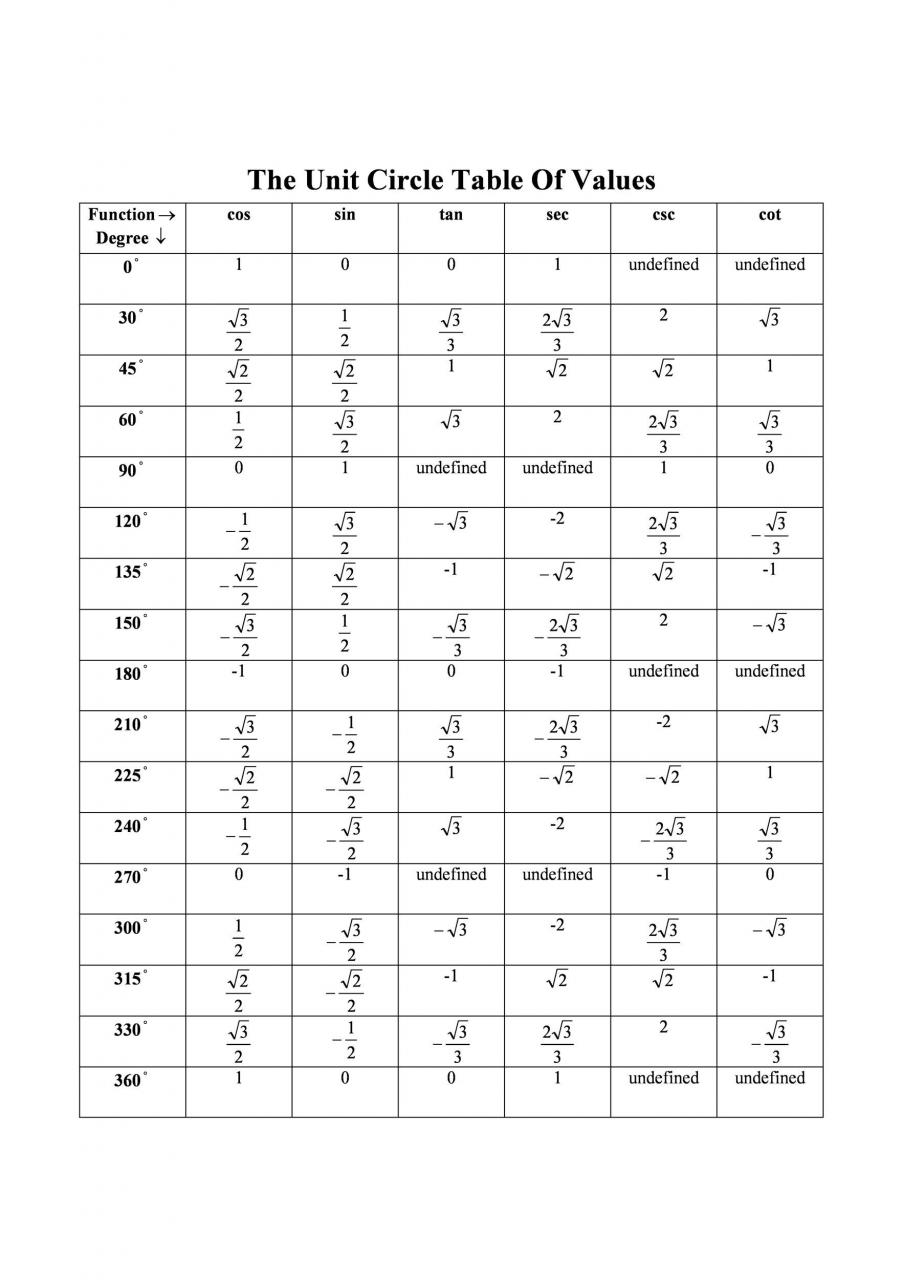
Todos estos son partes del círculo unitario completo. El gráfico del círculo unitario también incluye sen, cos, tan, sec, csc, cot. Afortunadamente, no tienes que memorizar todo lo relacionado con el círculo unitario completo.
Todo lo que necesitas hacer es aplicar los conceptos básicos que conoces sobre el círculo y sobre los triángulos rectángulos.
Comprender un gráfico de círculo unitario
Cuando se trata de trigonometría , puede usar un diagrama de círculo unitario. De hecho, es una de las mejores herramientas que puede utilizar. En lugar de hacer su propio círculo unitario, puede descargar un círculo unitario imprimible y trabajar con él.
O eso o hacer un círculo unitario en blanco para usar. Si puedes entender este concepto y lo que hace, la trigonometría será mucho más fácil. Usted será capaz de comprenderlo también. Aquí hay algunos tips para ayudarte:
Saber qué es un círculo unitario
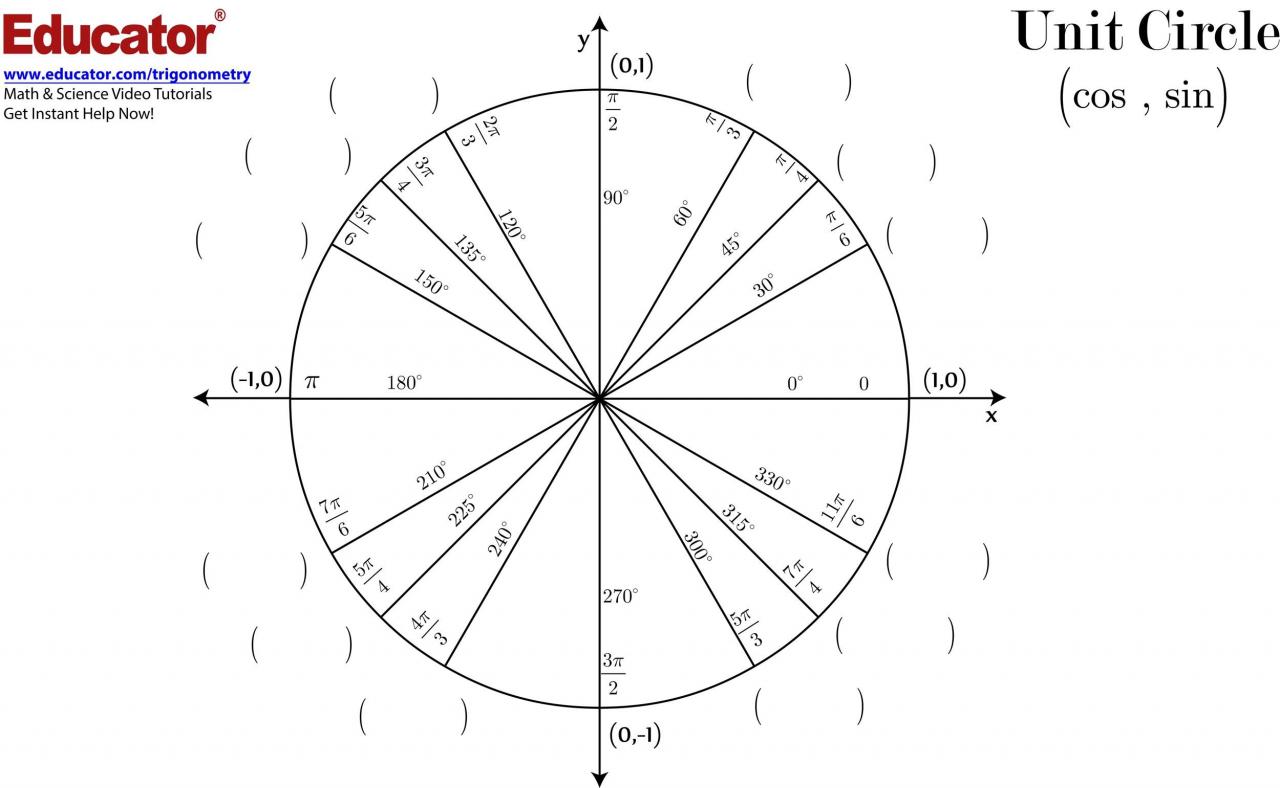
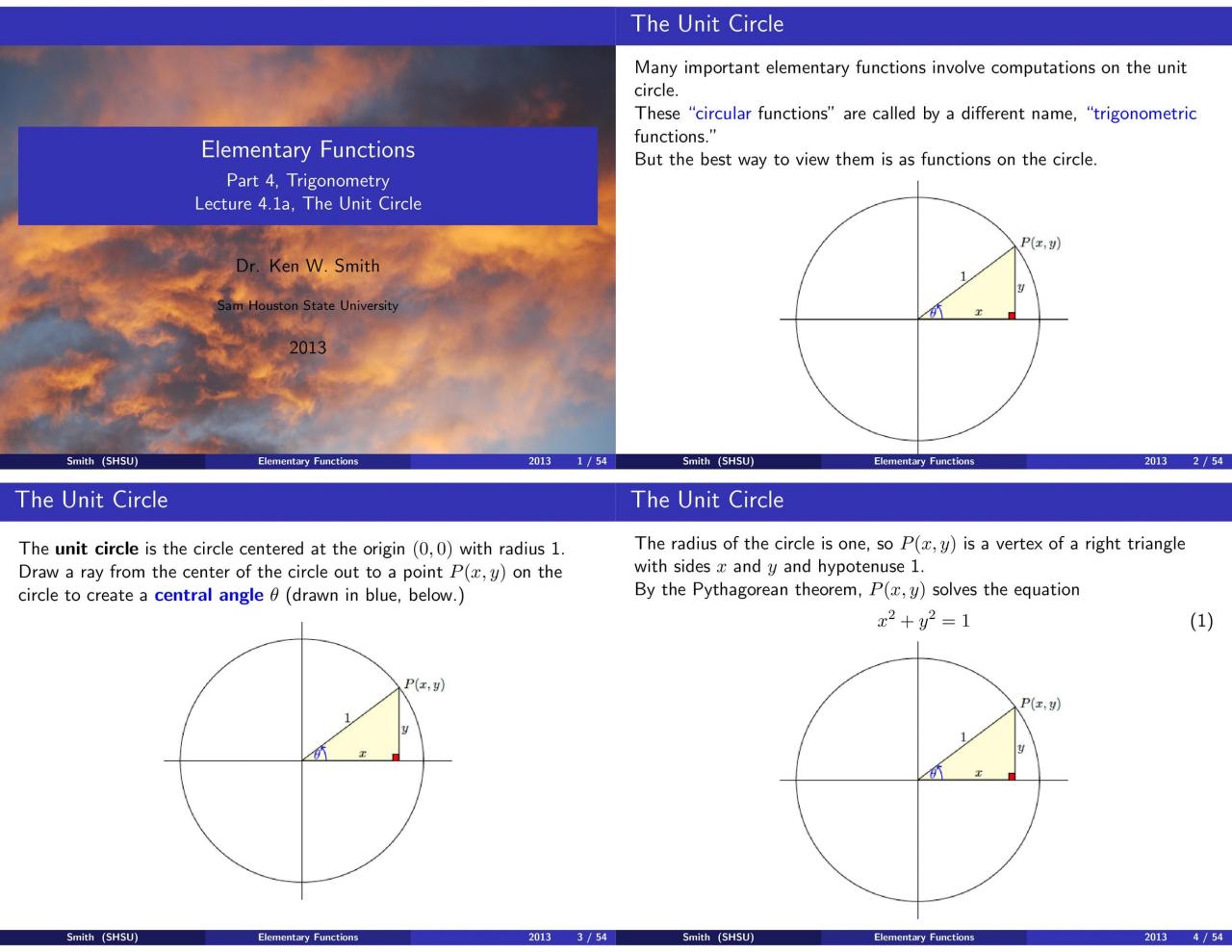
Antes de que puedas entenderlo, primero debes saber qué es. En realidad, un círculo unitario es simplemente un círculo con un radio de 1 que está centrado en el origen. Puede usar este círculo para encontrar funciones y proporciones trigonométricas especiales.
También puede usarlo para ayudarlo a trazar gráficos. También hay una recta numérica envuelta alrededor del círculo unitario. Esto sirve como valor de entrada cuando está evaluando funciones trigonométricas.
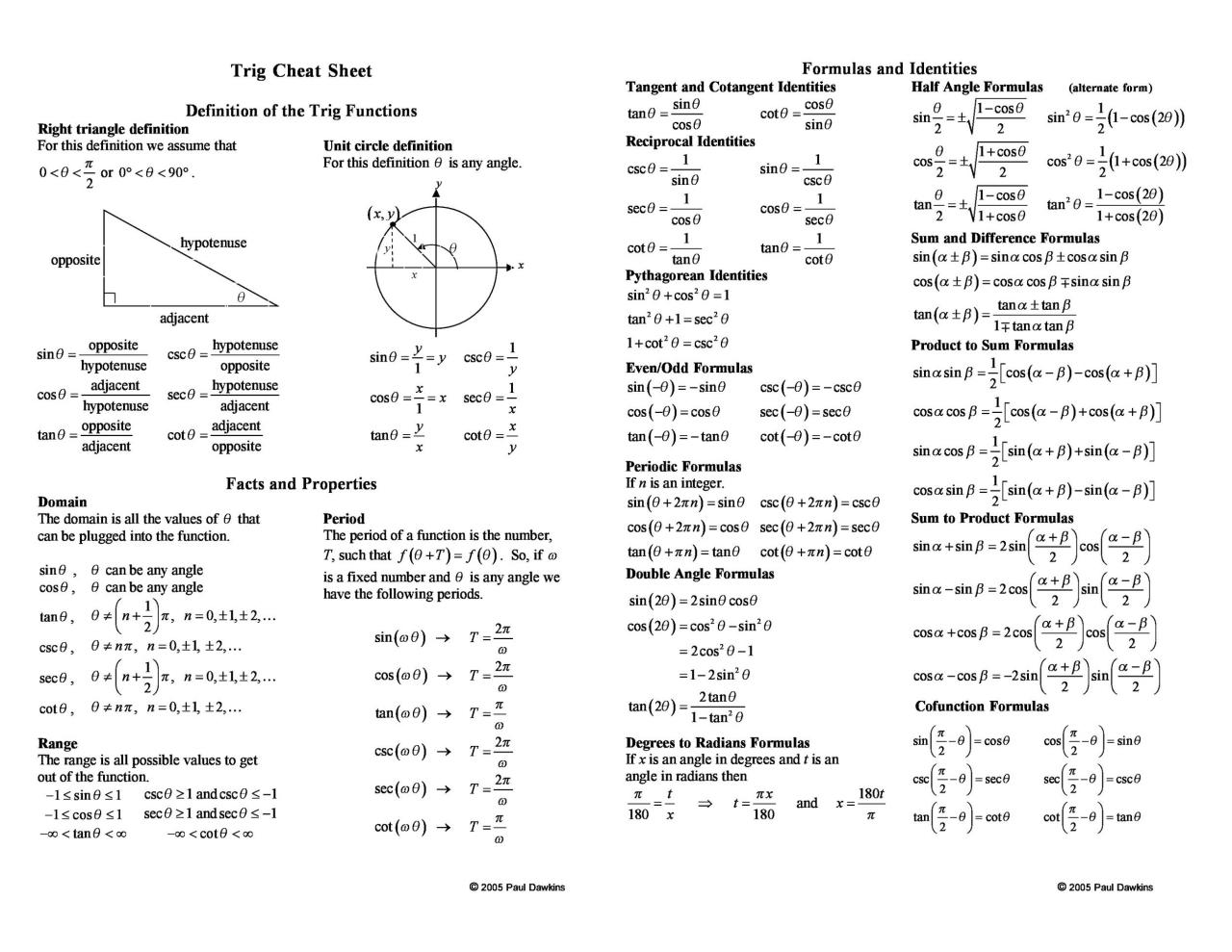
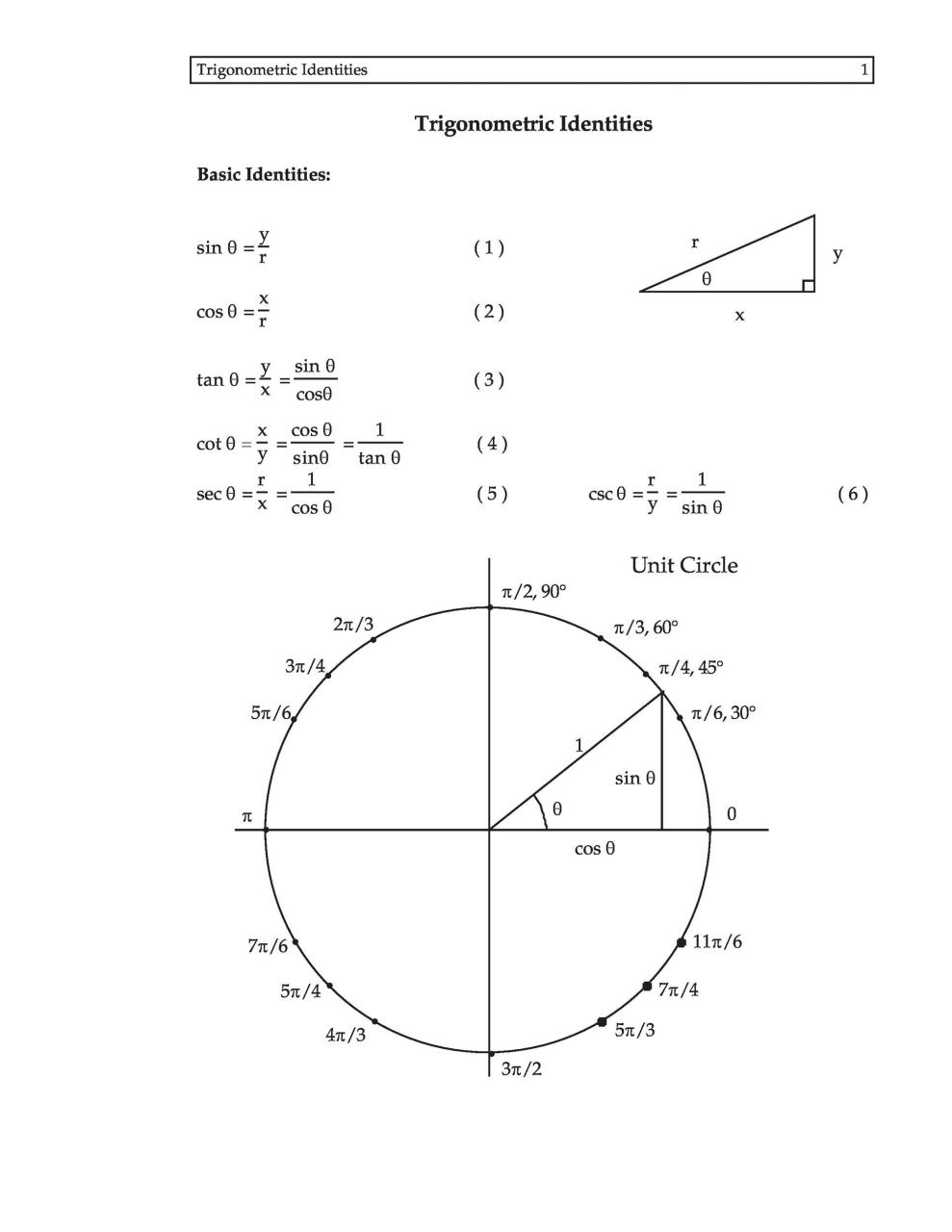
Conoce las 6 razones trigonométricas básicas
Un gráfico de círculo unitario tiene relaciones sen cos tan sec csc cot. Para entender el gráfico, necesitas conocerlos:
- sinθ es igual a opuesto/hipotenusa
- cosθ es igual a adyacente/hipotenusa
- tanθ es igual a opuesto/adyacente
- cscθ es igual a 1/sinθ
- secθ es igual a 1/cosθ
- cotθ es igual a 1/tanθ.
saber lo que es un radian
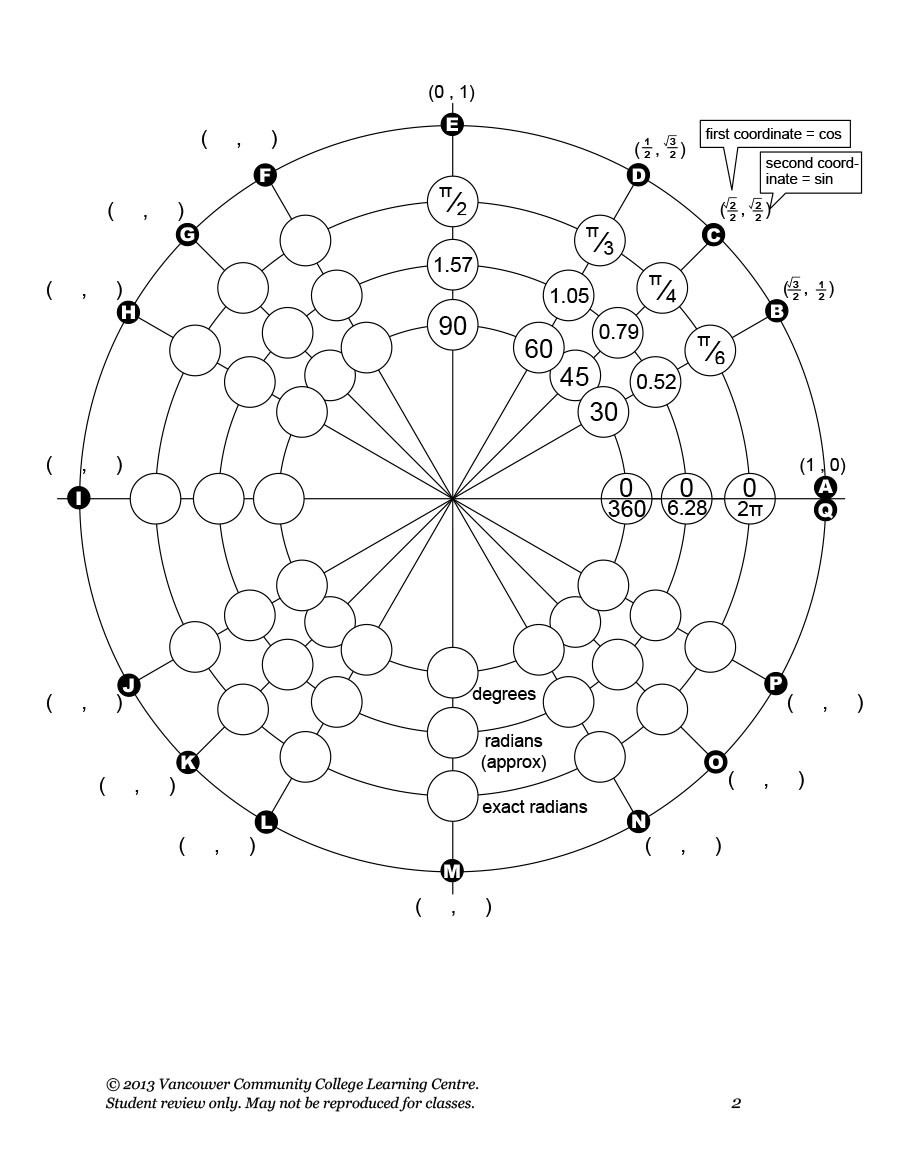
Por definición, un radián es una forma alternativa de medir ángulos. Un solo radián es un ángulo que necesitas. Entonces, la longitud del radio sería igual a la longitud del arco encerrado. El tamaño o la orientación del círculo no es significativo.
Sin embargo, debes saber cuántos radianes hay en todo el círculo. Para facilitarte las cosas, un círculo completo tiene 2π radianes.
Ser capaz de convertir de manera competente entre grados y radianes
Si desea comprender un gráfico circular en radianes, debe poder convertir valores de manera competente. En el último punto, hemos establecido que un círculo completo tiene 2π radianes. Así que aquí hay algunas conversiones rápidas para usted:
- 2πradian es igual a 360 grados y viceversa.
- Radian es igual a (360/2π) grado y viceversa.
- Radian es igual a (180/π) grado y viceversa.
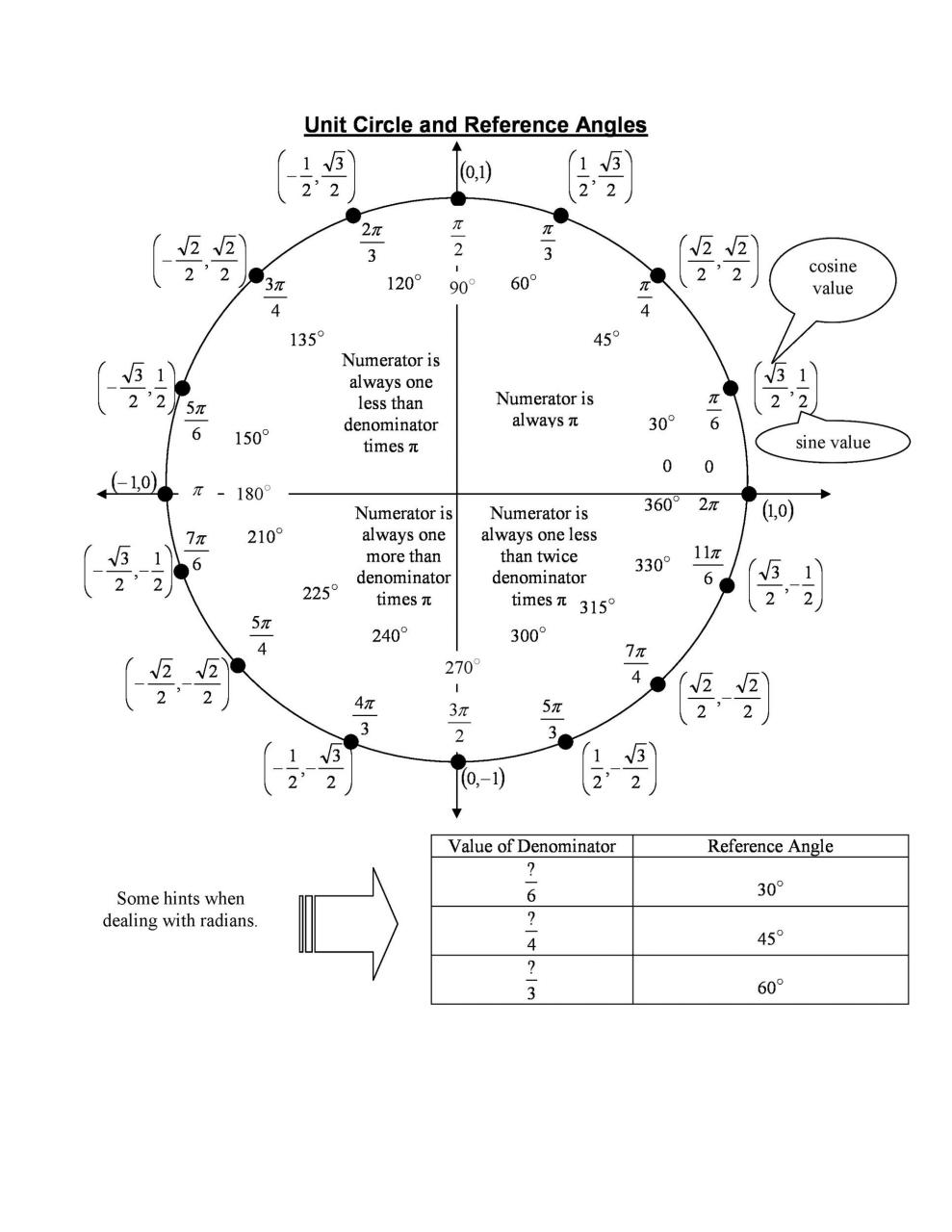
Conoce los ángulos “especiales”
Hay algunos ángulos especiales que necesitas saber y recordar. Estos son π/6, π/3, π/4, π/2, π y todos sus múltiplos.
Conocer y recordar las identidades trigonométricas que proporcionan las 6 funciones trigonométricas básicas para ángulos
Hay identidades trigonométricas que proporcionan las 6 funciones trigonométricas básicas para ángulos. Si desea comprender los círculos unitarios, las tablas y los diagramas , debe conocerlos. Aquí están las identidades de un gráfico de círculo unitario sen cos tan sec csc cot:
- senθ es igual a y
- cosθ es igual a x
- tanθ es igual a y/x
- csc es igual a 1/año
- segundo es igual a 1/x
- cuna es igual a x/y
Ubica y recuerda las 6 funciones trigonométricas básicas para los ángulos en los ejes
Es bastante fácil localizar las funciones trigonométricas de ángulos que son múltiplos de π/2. Estos incluyen 0, π/2, π, 3π/2, 2π, etc. Todo lo que necesitas hacer es imaginar el ángulo en los ejes. Si el lado terminal del ángulo está a lo largo del eje y, su seno será 1 o -1.
Entonces su cos será automáticamente 0. Por otro lado, si el lado terminal del ángulo está a lo largo del eje x, su seno será 0. Entonces su cos será 1 o -1.
Localiza y recuerda las 6 funciones trigonométricas básicas de π/6, que es un ángulo especial
Para hacer esto, comienza dibujando el ángulo π/6 en tu círculo unitario. Recuerda que los triángulos especiales tienen diferentes longitudes de lado. Estos son 45-45-90 y 30-60-90. El lado corto del triángulo es la mitad de la hipotenusa.
Esto significa que la coordenada y es igual a 1/2. Por otro lado, el lado largo es √3 veces el lado más corto o (√3)/2. Esto significa que la coordenada x es igual a (√3)/2. Entonces los puntos del ángulo especial son ((√3)/2,1/2). Entonces significa que:
- senπ/6 es igual a 1/2
- cosπ/6 es igual a (√3)/2
- tanπ/6 es igual a 1/(√3)
- cscπ/6 es igual a 2
- secπ/6 es igual a 2/(√3)
- cotπ/6 igual a √3
Ubica y recuerda las 6 funciones trigonométricas básicas de π/3, que es un ángulo especial
Este ángulo es menos complicado que el anterior. Tiene un punto en la circunferencia del círculo. En ese punto, la coordenada x es igual a la coordenada y en el ángulo π/6.
Para este ángulo, su coordenada y es idéntica a la coordenada x. Entonces el punto del ángulo es (1/2, √3/2). Entonces significa que :
- senπ/3 es igual a (√3)/2
- cosπ/3 es igual a 1/2
- tanπ/3 es igual a √3
- cscπ/3 es igual a 2/(√3)
- segπ/3 es igual a 2
- cotπ/3 es igual a 1/(√3)
Localiza y recuerda las 6 funciones trigonométricas básicas de π/4, que es un ángulo especial
Aquí hay otro ángulo especial para que lo recuerdes. Para este, usarás las proporciones de un triángulo 45-45-90. Tiene lados de 1 y una hipotenusa de √2. Entonces, si se trazan en un círculo unitario, las funciones trigonométricas básicas son:
- senπ/4 es igual a 1/(√2)
- cosπ/4 es igual a 1/(√2)
- tanπ/4 es igual a 1
- cscπ/4 es igual a √2
- secπ/4 igual a √2
- cotπ/4 es igual a 1
Sepa qué ángulo de referencia utilizar
En este punto, ya debería haber entendido los valores trigonométricos de los ángulos especiales. Estos ángulos de referencia especiales son π/6, π/3 y π/4. Pero todos estos ángulos están en el primer cuadrante.
Si necesita ubicar una función de un ángulo especial más pequeño o más grande, necesita saber qué ángulo de referencia usar. Generalmente, el ángulo de referencia que necesitas pertenece a la misma familia de ángulos.
Para determinar, necesitas reducir la fracción tanto como puedas. Después de eso, debe mirar el número en la parte inferior. Entonces:
- Si está solo, pertenece a la familia π
- Si es un 2, pertenece a la familia π/2
- Si es un 3, pertenece a la familia π/3
- Si es un 4, pertenece a la familia π/4
- Si es un 6, pertenece a la familia π/6
